
This tutorial covers different concepts related to neural networks with Sklearn and PyTorch. Neural networks have gained lots of attention in machine learning (ML) in the past decade with the development of deeper network architectures (known as deep learning).
These models have even surpassed human capabilities in different vision and natural language processing datasets. For example a neural network trained on the well-known ImageNet object recognition database tells the difference between different breeds of dog with an error rate of just 4.58%. For comparison, the typical human gets around 5%. Read more about this here.
In this tutorial, we will first see how easy it is to train multilayer perceptrons in Sklearn with the well-known handwritten dataset MNIST. Things will then get a bit more advanced with PyTorch. We will first train a network with four layers (deeper than the one we will use with Sklearn) to learn with the same dataset and then see a little bit on Bayesian (probabilistic) neural networks. This tutorial assumes some basic knowledge of python and neural networks.
If you are interested in the full code of this tutorial, download it from Maria’s Github here: https://github.com/mperezortiz/bayesianNNpytorch
What exactly are scikit-learn and PyTorch?
-
Scikit-learn is a free software machine learning library for Python which makes unbelievably easy to train traditional ML models such as Support Vector Machines or Multilayer Perceptrons.
-
PyTorch is an open source machine learning library based on Torch, used for coding deep learning algorithms and primarily developed by Facebook's artificial intelligence research group.
...and why should I care about Pytorch and Probabilistic Neural Networks?
-
Many people prefer PyTorch to TensorFlow. This is mainly because PyTorch allows for dynamic computational graphs (meaning that you can change the network architecture during running time, which is quite useful for certain neural network architectures) and it's very easy to learn (building ML models is actually very intuitive, as we will see).
-
ML needs to account for uncertainty! Have you heard of probabilistic programming? It's a programming paradigm in which you can easily specify probabilistic models and perform inference on them. These languages greatly simplify the task of creating systems that handle uncertainty. For example, Pyro (from Uber AI Labs) enables flexible and expressive deep probabilistic modelling, unifying the best of modern deep learning and Bayesian modelling. And while we won't touch on probabilistic programming in this tutorial, you may want to know why probabilistic approaches are so needed in ML and why these languages are growing so quickly. The network we are going to build doesn't use probabilistic programming languages, but it's still probabilistic!
Anyway... let's get to it, shall we?
Let's start with Sklearn and then we will move to PyTorch and finally include some notions of PNNs into the equation...
Multilayer Perceptron in Sklearn to classify handwritten digits
The dataset we are going to use (MNIST) is still one of the most used benchmarks in computer vision tasks, where one needs to go from an image of a handwritten digit to the digit itself (0, 1, 2...). This could be done with a Convolutional Neural Network, which are the state-of-the-art method for discovering spatial patterns. However, to simplify this tutorial what we will do is to unroll/flatten the image into a vector (images are 28x28 pixels, which will result in a vector of size 784, where each element represents a pixel) and use a fully connected neural network.
What we are aiming to do is to build a mathematical function that can predict the characteristic of interest (digit) based on the pixels. This is where neural networks come in handy, as they are mathematical functions that are universal approximators (can approximate any function given enough degrees of freedom). Neural networks implement linear functions. However, they can also include nonlinear transformations known as activation units (for example a logistic function), which allows them to provide non-linear decision regions!
Let's see how easy it would be to do so in Sklearn... We will build both a simple linear perceptron and a multilayer perceptron with the default activation functions in Sklearn, which are the so-called ReLU. When you run the code don't forget to compare the accuracy of both models and play around with the hyperparameters and network architecture!

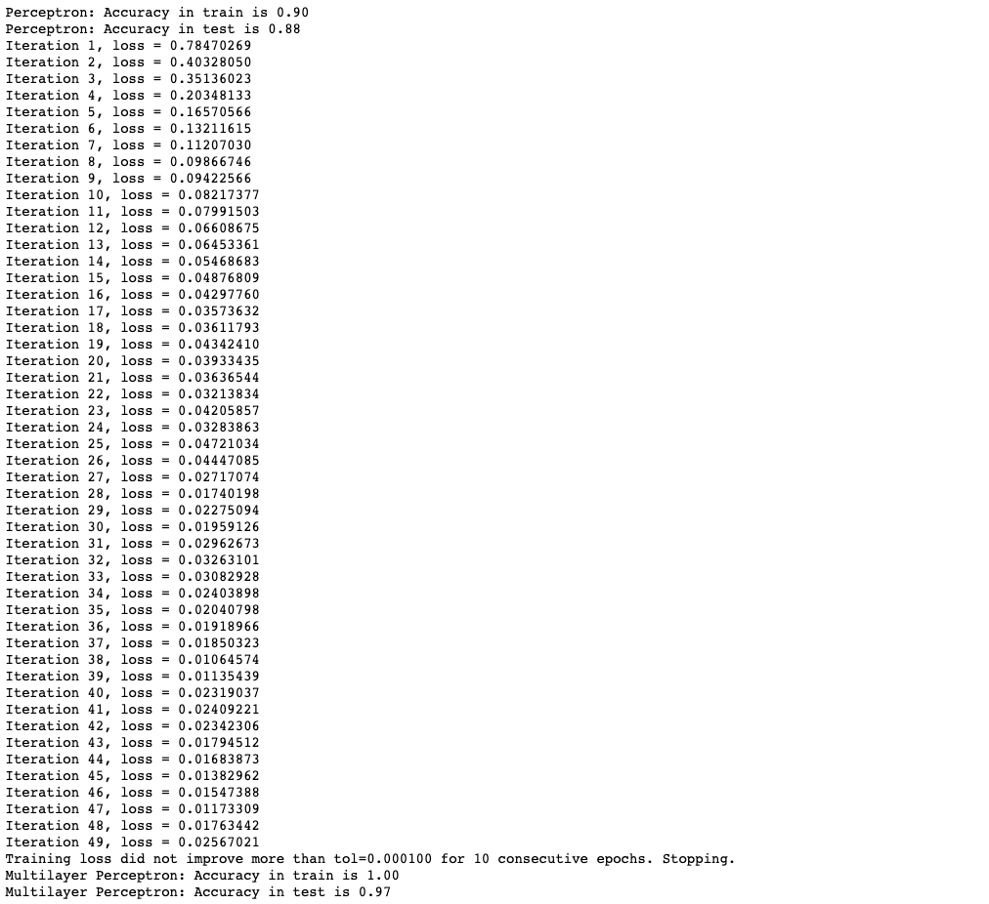
A standard Neural Network in PyTorch to classify MNIST
The Torch module provides all the necessary tensor operators you will need to build your first neural network in PyTorch. And yes, in PyTorch everything is a Tensor. This is because PyTorch is mostly used for deep learning, as opposed to Sklearn, which implements more traditional and shallower ML models.
Now we will use a similar architecture to the one we used before with Sklearn but deeper, this means that it will need to train many more parameters. We could have built exactly this same model in Sklearn, but it would have taken longer to train, as we will be using GPU to train our model in PyTorch. PyTorch would also be helpful when training more complex architectures (such as the previously mentioned Convolutional Neural Networks, which would be the ideal way of handling this computer vision dataset).
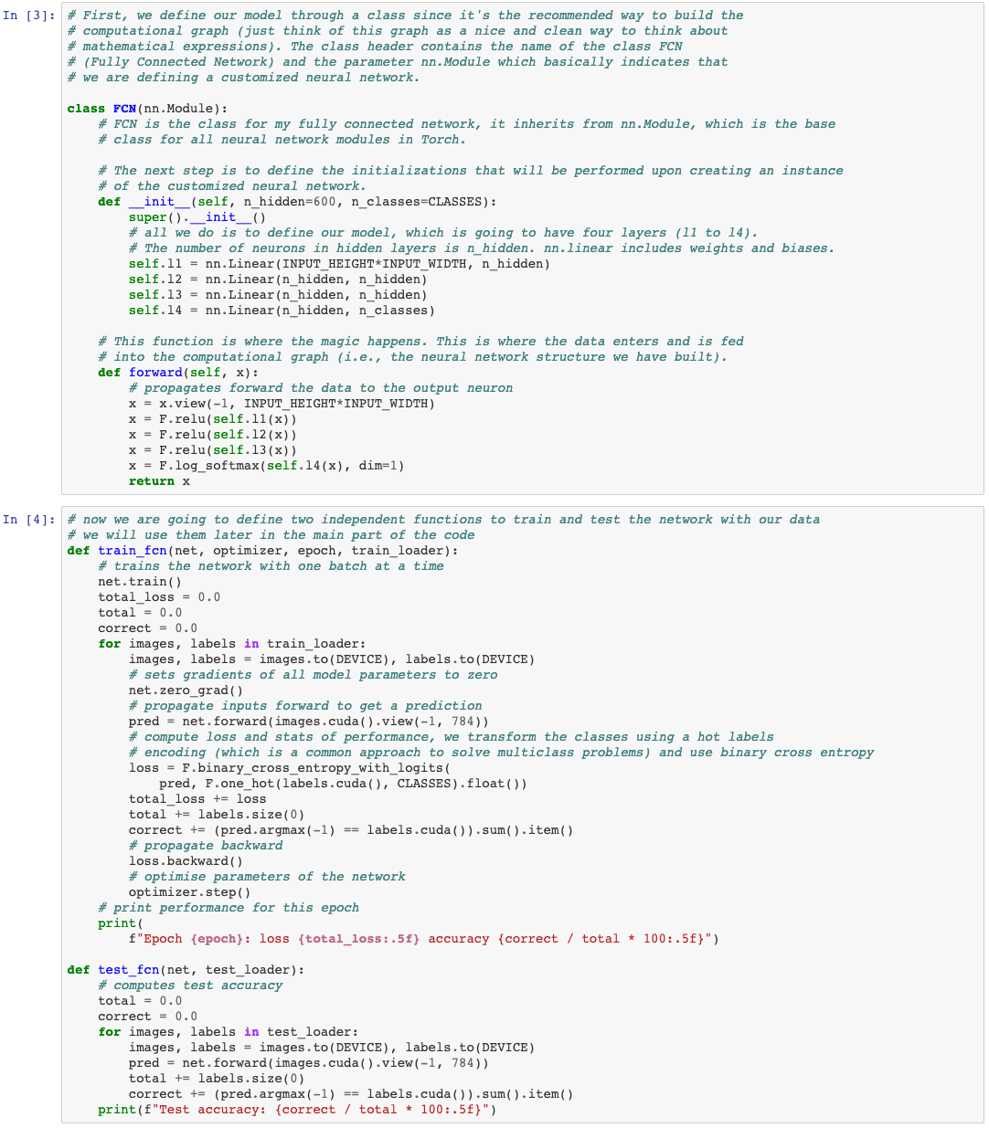
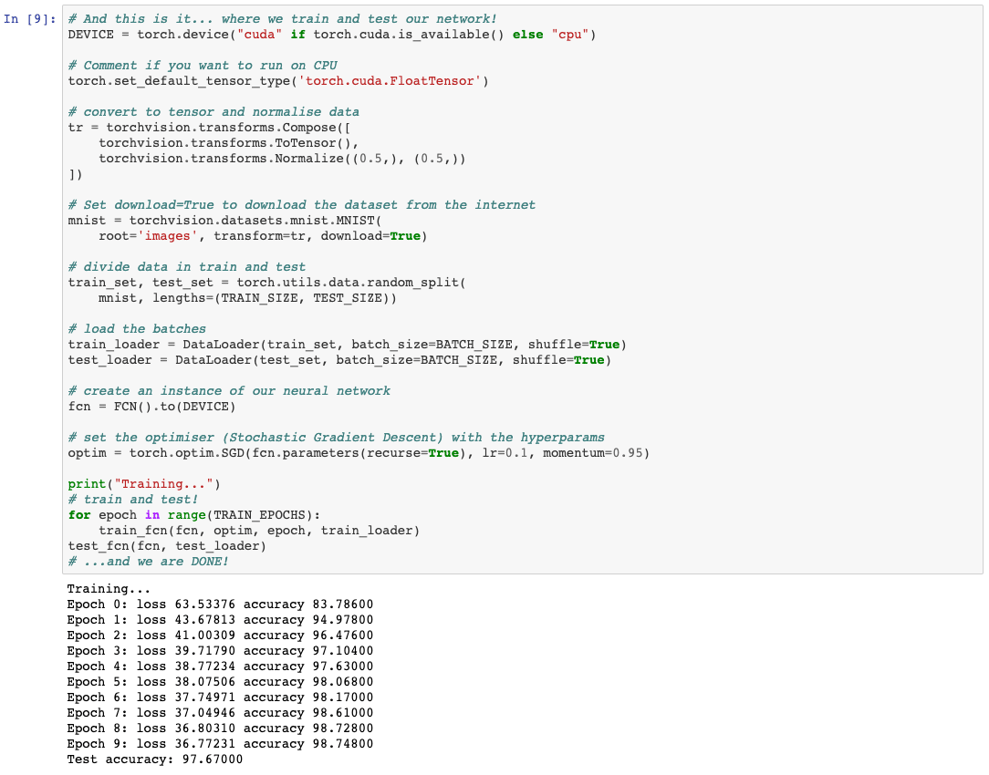 To recap... We defined the class with the architecture of our neural network, a train and test functions and the main part of our code (which was really simple: download data, partition, preprocess, set optimiser and hyperparameters and train and test). We can see that we achieve really good accuracy in test after training for 10 epochs. In this case, we used a network composed of 4 layers with ReLU activation functions, which seems to work really well for our dataset. However, these and other hyperparameters (such as learning rate) need to be optimised in order to find the best configuration for each specific problem. I will leave it to you to play with these hyperparameters and compare the accuracies of our network with for example 3 and 5 layers.
To recap... We defined the class with the architecture of our neural network, a train and test functions and the main part of our code (which was really simple: download data, partition, preprocess, set optimiser and hyperparameters and train and test). We can see that we achieve really good accuracy in test after training for 10 epochs. In this case, we used a network composed of 4 layers with ReLU activation functions, which seems to work really well for our dataset. However, these and other hyperparameters (such as learning rate) need to be optimised in order to find the best configuration for each specific problem. I will leave it to you to play with these hyperparameters and compare the accuracies of our network with for example 3 and 5 layers.
Now, let's move to the probabilistic version.
Wait a moment... What is a Probabilistic Neural Network anyway?
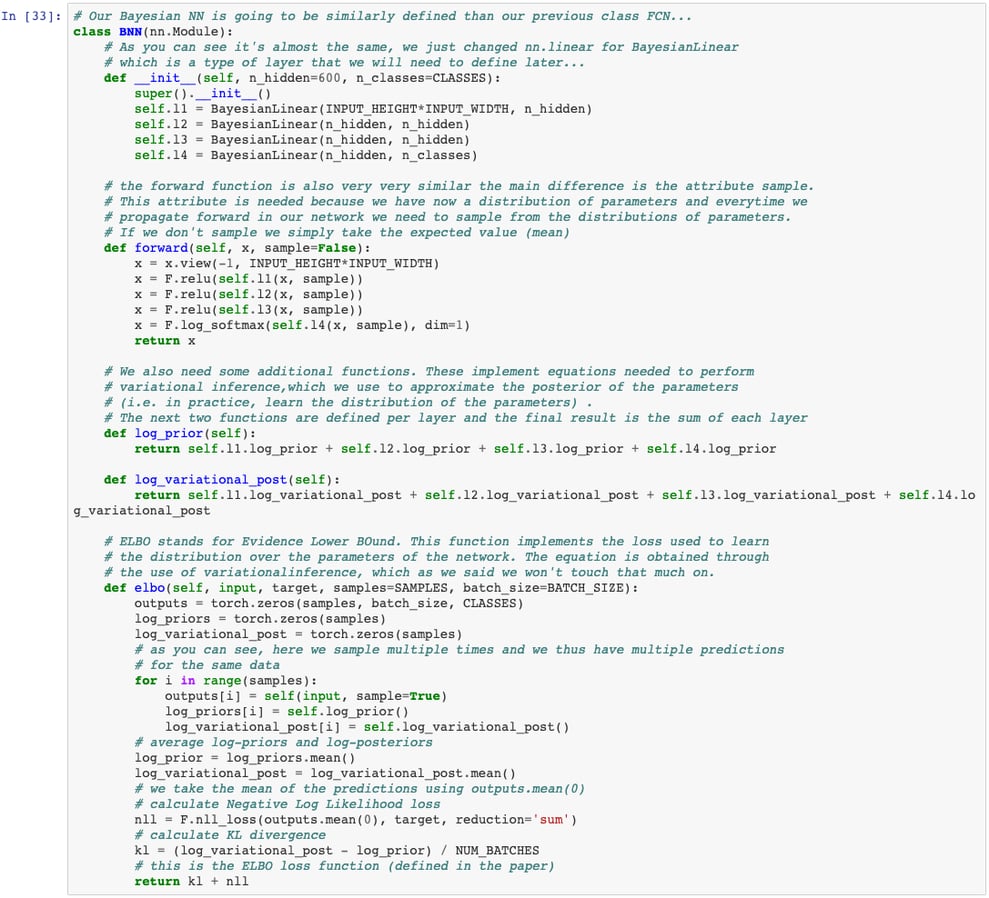
Bayesian neural networks (from now on BNNs) use the Bayes rule to create a probabilistic neural network. BNNs can be defined as feedforward neural networks that include notions of uncertainty in their parameters. Let us go back for a moment to the equation of a simple linear perceptron: y = W*X + b, where X is our input data and y our targets. The parameters to learn are W and b and these are usually optimised through maximum likelihood estimation. However, instead of having simply one scalar parameter for b (or any of the elements in W), we could learn a distribution (Normal, Laplace, etc.). In the case of a Normal distribution, we will then define each parameter with a mean and standard deviation. This is the idea behind the paper "Weight Uncertainty in Neural Networks" from Blundell et. al. at Google: The BNN learns a distribution for every network parameter.
This is useful for several reasons:
-
Firstly, it allows our network to produce uncertainty outcomes or even say "I don't know". Why is this important, you may ask? Just imagine that you have a system that distinguishes dogs from cats (what a cliché...), what do you think will happen if you input let's say a picture of yourself? Well, it's going to choose either dog and cat, which initially may sound cool, but let's face it, it's not very useful in practice. So the first advantage of a probabilistic neural network is to be able to say: "Actually, I'm not sure which class this test data point belongs to!"
-
The second cool advantage of BNNs is that they are easy to prune. For example, if after training our network we have a weight: 1) which mean is close to zero and 2) we are very sure about it (this is, uncertainty is very low) we can prune the neuron associated to it (easy peasy!). Pruning a model is usually important in real-world applications.
-
It regularises the weights, improving performance and yielding comparable performance to the commonly used dropout technique.
On the other hand, not everything is greener on the other side. BNNs tend to be slower than their non-probabilistic analogues at classifying new cases and they require more memory space to store the model.
Now... is building a BNN going to get much more difficult than our previous example? A bit, but let's clarify some concepts first.
-
The first thing you need to understand about these networks is that to test them with a data point we will need to sample from the distribution of parameters (or with the expected value otherwise). In practice, these network work then as an ensemble, producing multiple results for the same data point (this coming from the fact that we are sampling several times from the distribution of parameters). These outputs can be then averaged to get the final prediction and a notion of uncertainty in the prediction.
-
The second concept is that as the word Bayesian indicates, we impose a prior on the network parameters. We usually define the distribution (e.g. Normal) and we initalise the parameters with the prior. In this case, we use an engineered mixture of Gaussians for the prior.
Now, this tutorial will only give you an intuition of how BNNs work. We won't dive much deeper into variational inference, which is the approach these network use to approximate the distribution of learnt parameters. At this point, you just need to know that variational inference is one of the most common approaches (apart from sampling) to approximate a posterior distribution (you may have heard of variational autoencoders before). For more information please refer to the paper "Weight Uncertainty in Neural Networks" and get deeper into the theory behind it! The implementation in this paper is inspired by several other implementations of the same idea, specially the one in https://www.nitarshan.com/bayes-by-backprop/.
What we need for this code is to define 1. the architecture (number of layers + the definition of a Bayesian layer), 2. a loss function to define how to account for misclassification errors and use during learning and 3. the train and test functions.




Conclusions
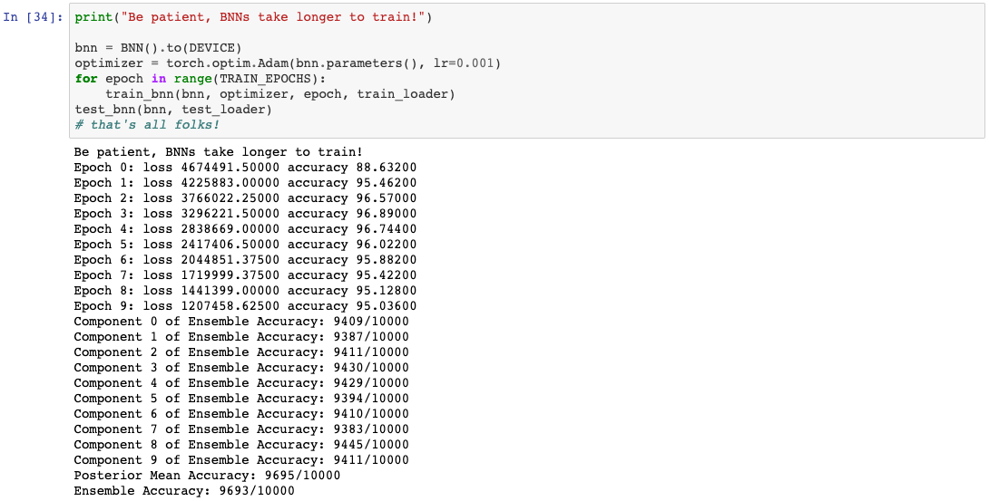
Now we can see that the test accuracy is similar for all three networks (the network with Sklearn achieved 97%, the non bayesian PyTorch version achieved 97.64% and our Bayesian implementation obtained 96.93%). This, however, is quite different if we train our BNN for longer, as these usually require more epochs. However, independently of the accuracy, our BNN will be much more useful. As we said before, we can prune the network easily and we have a notion of uncertainty in our predictions (which we generate by sampling many times). The fact that the network in Sklearn with a more shallower architecture performs as well as the deeper version might indicate that more layers are not necessary. But to be sure of this we would need to explore much better the performance of these networks by testing different hyperparameter configuration.
Now the question is: How do we include the reject option in our network? (this is, allow it to say "I don't know"): Well, again, we will sample many times (perhaps more than 10, let's say 100), which will give us a much better estimation of the probability of a digit belonging to a class. Then we will need to set a threshold (let's say 0.2) and we will reject classifying every digit for which at least we are not a 20% sure that it belongs to a specific class! This is, if the network is not confident up to a threshold in its prediction, it will reject classifying that example. If you are interested in taking a better look at how to do this I recommend this tutorial.
In this tutorial we have implemented three multilayer perceptrons with the well-known ReLU activation function, one with Sklearn and two with PyTorch and used one of the most well-known datasets in computer vision (MNIST, for handwritten digit recognition). We have also learnt about the usefulness of probabilistic neural networks and got some intuition about how to implement these!
More Tutorials to Practice your Skills on:
– Introduction to Missing Data Imputation
– Hyperparameter tuning in XGBoost
– Introduction to CoordConv Architecture: Deep Learning
– Unit testing with PySpark
– Getting started with XGBoost

About the author:
Maria received her PhD in Computer Science from the University of Cordoba (Spain) in 2015. Since then, she has worked at Cambridge University and University College London as postdoctoral research fellow, with a focus on machine learning and computer vision.
Discover Cambridge Spark's Data Science programmes
Get in touch below to find out more about our Data Science programmes including our advanced Level 7 AI and Data Science apprenticeship and start the journey to upskill you and your team today:
-1.png)
Enquire now
Fill out the following form and we’ll contact you within one business day to discuss and answer any questions you have about the programme. We look forward to speaking with you.
